| Latest Maths NCERT Books Solution | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
| Content On This Page | ||
|---|---|---|
| Example 1 to 3 (Before Exercise 10.1) | Exercise 10.1 | |
Chapter 10 Heron's Formula
Welcome to the focused solutions guide for Chapter 10, "Heron's Formula," from the latest Class 9 NCERT mathematics textbook for the academic session 2024-25. This chapter introduces a remarkably useful formula attributed to Heron of Alexandria, providing a powerful method to calculate the area of a triangle when only the lengths of its three sides are known. This is particularly advantageous when the height (altitude) of the triangle is not given or is difficult to determine, offering an alternative to the standard Area = $\frac{1}{2} \times \text{base} \times \text{height}$ formula. These solutions provide comprehensive, step-by-step assistance in applying Heron's formula accurately and effectively to various problems.
The core of this chapter revolves around understanding and applying Heron's Formula. The solutions clearly introduce the formula itself. For a triangle with side lengths $a$, $b$, and $c$, the area ($A$) is calculated as follows:
- First, calculate the semi-perimeter ($s$) of the triangle: $s = \frac{a+b+c}{2}$.
- Then, apply Heron's Formula: $A = \sqrt{s(s-a)(s-b)(s-c)}$.
A key application highlighted in the solutions is using Heron's formula to find the area of quadrilaterals or other polygons. This is achieved by dividing the polygon into constituent triangles using one or more diagonals. If the side lengths of these resulting triangles are known (or can be determined – perhaps using the Pythagorean theorem if a right-angled triangle is formed within the quadrilateral), Heron's formula can be applied to each triangle individually. The total area of the polygon is then found by summing the areas of these triangles. The solutions provide clear illustrations of this strategy, breaking down the process into manageable steps.
Furthermore, the solutions address practical word problems that often involve finding the area of triangular fields, plots of land, or other real-world shapes where side lengths are the primary information provided. These problems test the student's ability to extract the side lengths from the problem description and apply Heron's formula correctly, sometimes involving calculations with units (like $m^2$) or costs associated with the area (e.g., cost of leveling a field at a certain rate per square meter, potentially using $\textsf{₹}$).
Regarding the rationalized syllabus for 2024-25, Chapter 10, "Heron's Formula" (formerly Chapter 12), has been retained in the Class 9 NCERT curriculum. Its focus remains squarely on the introduction and application of Heron's formula for finding the area of triangles and its use in calculating the area of quadrilaterals by division into triangles. The rationalization process primarily involved ensuring the exercises focus directly on these core applications without excessive complexity in calculations or contexts. By diligently working through these detailed solutions, students can master the precise application of Heron's formula, perform the calculations accurately, and confidently solve problems involving the area of triangles and related composite shapes based on given side lengths.
Example 1 to 3 (Before Exercise 10.1)
Example 1. Find the area of a triangle, two sides of which are 8 cm and 11 cm and the perimeter is 32 cm (see Fig. 10.3).
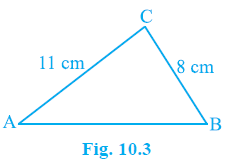
Answer:
Given:
Two sides of the triangle are $a = 8$ cm and $b = 11$ cm.
Perimeter of the triangle = 32 cm.
To Find:
Area of the triangle.
Solution:
Let the third side of the triangle be $c$ cm.
The perimeter of a triangle is the sum of its three sides.
Perimeter = $a + b + c$
Substitute the given values:
$32 = 8 + 11 + c$
$32 = 19 + c$
Subtract 19 from both sides to find $c$:
$c = 32 - 19$
$c = 13$ cm
The third side of the triangle is 13 cm.
Now, we calculate the semi-perimeter ($s$).
$s = \frac{\text{Perimeter}}{2}$
$s = \frac{32}{2}$
$s = 16$ cm
Using Heron's formula, the area of a triangle with sides a, b, c and semi-perimeter s is given by:
$\text{Area} = \sqrt{s(s-a)(s-b)(s-c)}$
Substitute the values of s, a, b, and c:
$\text{Area} = \sqrt{16(16-8)(16-11)(16-13)}$
$\text{Area} = \sqrt{16(8)(5)(3)}$
$\text{Area} = \sqrt{16 \times 8 \times 5 \times 3}$
$\text{Area} = \sqrt{16 \times 120}$
$\text{Area} = \sqrt{1920}$
$\text{Area} = \sqrt{64 \times 30}$
$\text{Area} = \sqrt{64} \times \sqrt{30}$
$\text{Area} = 8 \times \sqrt{30}$
$\text{Area} = 8\sqrt{30}$ cm$^2$
The area of the triangle is $8\sqrt{30}$ cm$^2$.
The final answer is $8\sqrt{30}$ cm$^2$.
Example 2. A triangular park ABC has sides 120m, 80m and 50m (see Fig. 10.4). A gardener Dhania has to put a fence all around it and also plant grass inside. How much area does she need to plant? Find the cost of fencing it with barbed wire at the rate of ₹ 20 per metre leaving a space 3m wide for a gate on one side.
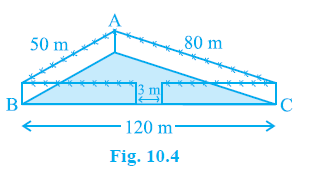
Answer:
Given:
The sides of the triangular park ABC are $a = 120$ m, $b = 80$ m, and $c = 50$ m.
Rate of fencing = $\textsf{₹}$ 20 per metre.
Space left for a gate = 3 m.
To Find:
The area required to plant grass.
The cost of fencing.
Solution:
To find the area required to plant grass, we use Heron's formula.
First, calculate the semi-perimeter ($s$) of the triangular park.
$s = \frac{a + b + c}{2}$
$s = \frac{120 + 80 + 50}{2}$
$s = \frac{250}{2}$
$s = 125$ m
Now, calculate $s-a$, $s-b$, and $s-c$:
$s - a = 125 - 120 = 5$ m
$s - b = 125 - 80 = 45$ m
$s - c = 125 - 50 = 75$ m
Using Heron's formula for the area of the triangle:
$\text{Area} = \sqrt{s(s-a)(s-b)(s-c)}$
Substitute the values:
$\text{Area} = \sqrt{125 \times 5 \times 45 \times 75}$
$\text{Area} = \sqrt{(5^3) \times 5 \times (3^2 \times 5) \times (3 \times 5^2)}$
$\text{Area} = \sqrt{3^2 \times 3 \times 5^3 \times 5^1 \times 5^1 \times 5^2}$
$\text{Area} = \sqrt{3^3 \times 5^7}$
$\text{Area} = \sqrt{3^2 \times 3 \times 5^6 \times 5}$
$\text{Area} = \sqrt{3^2} \times \sqrt{5^6} \times \sqrt{3 \times 5}$
$\text{Area} = 3 \times 5^3 \times \sqrt{15}$
$\text{Area} = 3 \times 125 \times \sqrt{15}$
$\text{Area} = 375\sqrt{15}$ m$^2$
The area needed to plant grass is $375\sqrt{15}$ m$^2$.
To find the cost of fencing, we first find the total perimeter.
Total Perimeter = $a + b + c$
Total Perimeter = $120 + 80 + 50$
Total Perimeter = $250$ m
A space of 3m is left for a gate, so the length of the fence required is:
Length of fence = Total Perimeter - Gate space
Length of fence = $250$ m - $3$ m
Length of fence = $247$ m
The cost of fencing is the length of the fence multiplied by the rate per metre.
Cost of fencing = Length of fence $\times$ Rate
Cost of fencing = $247 \times \textsf{₹} 20$
Cost of fencing = $\textsf{₹} 4940$
Final Answer:
The area needed to plant grass is $375\sqrt{15}$ m$^2$.
The cost of fencing is $\textsf{₹} 4940$.
Example 3. The sides of a triangular plot are in the ratio of 3 : 5 : 7 and its perimeter is 300 m. Find its area.
Answer:
Given:
Ratio of the sides of the triangular plot is $3 : 5 : 7$.
Perimeter of the triangular plot is $300$ m.
To Find:
The area of the triangular plot.
Solution:
Let the sides of the triangular plot be $a=3x$, $b=5x$, and $c=7x$ metres, where $x$ is a positive constant.
The perimeter of the triangle is the sum of its sides.
$a + b + c = \text{Perimeter}$
… (i)
Substitute the expressions for the sides:
$3x + 5x + 7x = 300$
Combine the terms on the left side:
$(3+5+7)x = 300$
$15x = 300$
… (ii)
Divide both sides by $15$ to solve for $x$:
$x = \frac{300}{15}$
… (iii)
$x = 20$
… (iv)
Now, we find the actual lengths of the sides using the value of $x=20$ m.
$a = 3x = 3 \times 20 = 60$ m
$b = 5x = 5 \times 20 = 100$ m
$c = 7x = 7 \times 20 = 140$ m
The sides of the triangular plot are $60$ m, $100$ m, and $140$ m.
To find the area of the triangle, we will use Heron's formula. First, calculate the semi-perimeter, $s$.
$s = \frac{\text{Perimeter}}{2}$
$s = \frac{300}{2}$
… (v)
$s = 150$ m
… (vi)
Next, calculate the differences between the semi-perimeter and each side:
$s-a = 150 - 60 = 90$ m
$s-b = 150 - 100 = 50$ m
$s-c = 150 - 140 = 10$ m
Heron's formula for the area of a triangle with sides $a, b, c$ and semi-perimeter $s$ is:
Area $= \sqrt{s(s-a)(s-b)(s-c)}$
Substitute the values we calculated:
Area $= \sqrt{150 \times 90 \times 50 \times 10}$
… (vii)
Multiply the terms inside the square root:
Area $= \sqrt{6,750,000}$
… (viii)
Simplify the square root:
Area $= \sqrt{675 \times 10,000}$
Area $= \sqrt{225 \times 3 \times 100^2}$
(Since $675 = 225 \times 3$ and $10000 = 100^2$)
Area $= \sqrt{15^2 \times 3 \times 100^2}$
(Since $225 = 15^2$)
Area $= 15 \times 100 \times \sqrt{3}$
(Taking terms out of the square root)
Area $= 1500\sqrt{3} \, \text{m}^2$
… (ix)
The area of the triangular plot is $1500\sqrt{3}$ square metres.
Exercise 10.1
Question 1. A traffic signal board, indicating ‘SCHOOL AHEAD’, is an equilateral triangle with side ‘a’. Find the area of the signal board, using Heron’s formula. If its perimeter is 180 cm, what will be the area of the signal board?
Answer:
Given:
A traffic signal board in the shape of an equilateral triangle with side length '$a$'.
The perimeter of the signal board is $180$ cm (for the second part of the question).
To Find:
1. The area of the signal board using Heron’s formula in terms of '$a$'.
2. The area of the signal board if its perimeter is $180$ cm.
Solution:
The signal board is an equilateral triangle with sides of length $a, a, a$.
The perimeter of the equilateral triangle is the sum of its sides: Perimeter $= a + a + a = 3a$.
Part 1: Area of an equilateral triangle with side 'a' using Heron's formula.
Heron's formula states that the area of a triangle with sides $a', b', c'$ and semi-perimeter $s$ is given by Area $= \sqrt{s(s-a')(s-b')(s-c')}$.
In this case, the sides are $a' = a, b' = a, c' = a$.
The semi-perimeter $s$ is half of the perimeter:
$s = \frac{3a}{2}$
... (i)
Now we calculate $(s-a'), (s-b'),$ and $(s-c')$:
$s-a = \frac{3a}{2} - a = \frac{3a-2a}{2} = \frac{a}{2}$
$s-a = \frac{a}{2}$
$s-a = \frac{a}{2}$
Using Heron's formula for the equilateral triangle with sides $a, a, a$:
Area $= \sqrt{s(s-a)(s-a)(s-a)}$
... (ii)
Substitute the values of $s$ from (i) and $(s-a)$:
Area $= \sqrt{\frac{3a}{2} \times \frac{a}{2} \times \frac{a}{2} \times \frac{a}{2}}$
... (iii)
Simplify the expression inside the square root:
Area $= \sqrt{\frac{3a^4}{16}}$
... (iv)
Take the square root:
Area $= \sqrt{\frac{3}{16}} \times \sqrt{a^4}$
... (v)
Area $= \frac{\sqrt{3}}{4} \times a^2$
... (vi)
Area of equilateral triangle with side 'a' $= \frac{\sqrt{3}}{4} a^2$
$\$$ (Using Heron's formula) ... (vii)
Part 2: Area when perimeter is 180 cm.
Given that the perimeter of the equilateral triangle is $180$ cm.
Let the side length of the equilateral triangle be $a$ cm.
Perimeter $= 3a$
$3a = 180 \, \text{cm}$
... (viii)
Divide both sides by 3 to find the side length $a$:
$a = \frac{180}{3} \, \text{cm}$
... (ix)
$a = 60 \, \text{cm}$
... (x)
Now we can find the area using the formula derived in Part 1 (Equation vii), which was found using Heron's formula.
Area $= \frac{\sqrt{3}}{4} a^2$
$\$$ (From equation (vii)) ... (xi)
Substitute the value $a=60$ cm from (x):
Area $= \frac{\sqrt{3}}{4} (60)^2$
... (xii)
Area $= \frac{\sqrt{3}}{4} \times 3600$
... (xiii)
Cancel the 4 in the denominator with 3600:
Area $= \sqrt{3} \times \frac{\cancel{3600}^{900}}{\cancel{4}_{1}}$
... (xiv)
Area $= 900\sqrt{3} \, \text{cm}^2$
... (xv)
Final Answer:
The area of the signal board with side 'a' using Heron's formula is $\frac{\sqrt{3}}{4} a^2$.
The area of the signal board with perimeter 180 cm is $900\sqrt{3} \, \text{cm}^2$.
Question 2. The triangular side walls of a flyover have been used for advertisements. The sides of the walls are 122 m, 22 m and 120 m (see Fig. 10.6). The advertisements yield an earning of ₹ 5000 per m2 per year. A company hired one of its walls for 3 months. How much rent did it pay?
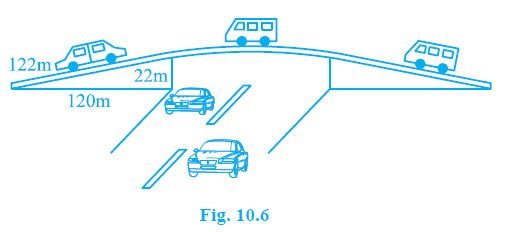
Answer:
Given:
Sides of the triangular side walls of a flyover are $a = 122$ m, $b = 22$ m, and $c = 120$ m.
Advertisement earning rate = $\textsf{₹} \ 5000$ per m$^2$ per year.
Duration for which a company hired the wall = $3$ months.
To Find:
The total rent paid by the company for $3$ months.
Solution:
First, we need to find the area of the triangular wall using Heron's formula. The sides of the triangle are $a = 122$ m, $b = 22$ m, and $c = 120$ m.
Calculate the semi-perimeter, $s$, of the triangle.
$s = \frac{a+b+c}{2}$
$s = \frac{122 + 22 + 120}{2}$
... (i)
$s = \frac{264}{2}$
... (ii)
$s = 132 \, \text{m}$
... (iii)
Now, calculate the differences between the semi-perimeter and each side:
$s-a = 132 - 122 = 10$ m
$s-b = 132 - 22 = 110$ m
$s-c = 132 - 120 = 12$ m
Using Heron's formula, the area of the triangle is:
Area $= \sqrt{s(s-a)(s-b)(s-c)}$
Substitute the values:
Area $= \sqrt{132 \times 10 \times 110 \times 12}$
... (iv)
To simplify the square root, factorize the numbers:
$132 = 11 \times 12$
$10 = 10$
$110 = 11 \times 10$
$12 = 12$
Area $= \sqrt{(11 \times 12) \times 10 \times (11 \times 10) \times 12}$
... (v)
Group identical factors:
Area $= \sqrt{11^2 \times 12^2 \times 10^2}$
... (vi)
Take the factors out of the square root:
Area $= 11 \times 12 \times 10$
... (vii)
Area $= 1320 \, \text{m}^2$
... (viii)
The area of the triangular wall is $1320$ m$^2$.
The advertisement rate is $\textsf{₹} \ 5000$ per m$^2$ per year.
The company hired the wall for $3$ months.
Convert the duration from months to years:
Duration in years $= \frac{3 \text{ months}}{12 \text{ months/year}}$
... (ix)
Duration in years $= \frac{\cancel{3}^1}{\cancel{12}_4}$ year
... (x)
Duration in years $= \frac{1}{4}$ year
... (xi)
The rent for the wall is calculated by multiplying the area by the rate per m$^2$ per year and the duration in years.
Total Rent = Area $\times$ Rate per m$^2$ per year $\times$ Duration in years
Total Rent $= 1320 \, \text{m}^2 \times \textsf{₹} \ 5000 \, \text{/m}^2/\text{year} \times \frac{1}{4} \, \text{year}$
... (xii)
Total Rent $= \textsf{₹} \ 1320 \times 5000 \times \frac{1}{4}$
... (xiii)
Simplify the calculation:
Total Rent $= \textsf{₹} \ \cancel{1320}^{330} \times 5000 \times \frac{1}{\cancel{4}_{1}}$
... (xiv)
Total Rent $= \textsf{₹} \ 330 \times 5000$
... (xv)
Total Rent $= \textsf{₹} \ 1,650,000$
... (xvi)
The company paid a rent of $\textsf{₹} \ 1,650,000$ for hiring the wall for $3$ months.
Question 3. There is a slide in a park. One of its side walls has been painted in some colour with a message “KEEP THE PARK GREEN AND CLEAN” (see Fig. 10.7). If the sides of the wall are 15 m, 11 m and 6 m, find the area painted in colour.
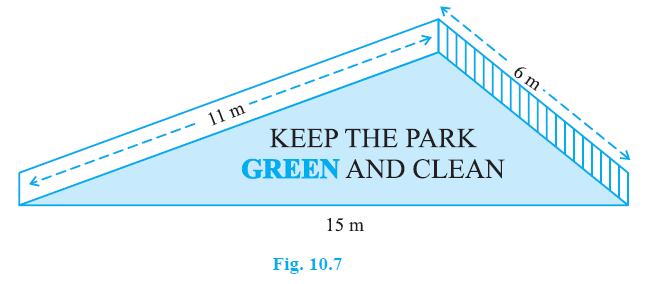
Answer:
Given:
The sides of the triangular side wall are $a = 15$ m, $b = 11$ m, and $c = 6$ m.
To Find:
The area of the wall painted in colour.
Solution:
The wall is in the shape of a triangle with side lengths $a = 15$ m, $b = 11$ m, and $c = 6$ m.
We can find the area of this triangle using Heron's formula.
First, calculate the semi-perimeter, $s$.
$s = \frac{a+b+c}{2}$
$s = \frac{15 + 11 + 6}{2}$
... (i)
$s = \frac{32}{2}$
... (ii)
$s = 16 \, \text{m}$
... (iii)
Next, calculate the differences between the semi-perimeter and each side:
$s-a = 16 - 15 = 1$ m
$s-b = 16 - 11 = 5$ m
$s-c = 16 - 6 = 10$ m
Using Heron's formula, the area of the triangle is:
Area $= \sqrt{s(s-a)(s-b)(s-c)}$
Substitute the calculated values:
Area $= \sqrt{16 \times 1 \times 5 \times 10}$
... (iv)
Multiply the terms inside the square root:
Area $= \sqrt{16 \times 50}$
... (v)
Simplify the square root by factoring:
Area $= \sqrt{16 \times 25 \times 2}$
$\$$ (Since $50 = 25 \times 2$)
Area $= \sqrt{16} \times \sqrt{25} \times \sqrt{2}$
... (vi)
Area $= 4 \times 5 \times \sqrt{2}$
... (vii)
Area $= 20\sqrt{2} \, \text{m}^2$
... (viii)
The area painted in colour on the side wall is $20\sqrt{2}$ square metres.
Question 4. Find the area of a triangle two sides of which are 18 cm and 10 cm and the perimeter is 42 cm.
Answer:
Given:
Let the sides of the triangle be $a$, $b$, and $c$.
Two sides are $a = 18$ cm and $b = 10$ cm.
Perimeter $P = 42$ cm.
To Find:
The area of the triangle.
Solution:
The perimeter of a triangle is the sum of its three sides.
$P = a + b + c$
We are given $P = 42$ cm, $a = 18$ cm, and $b = 10$ cm.
Substituting the given values:
$42 = 18 + 10 + c$
... (i)
$42 = 28 + c$
Now, we can find the third side $c$:
$c = 42 - 28$
$c = 14$ cm
Next, we find the semi-perimeter ($s$) of the triangle, which is half of the perimeter.
$s = \frac{P}{2}$
$s = \frac{42}{2}$
$s = 21$ cm
We can find the area of the triangle using Heron's formula, which is given by:
Area $= \sqrt{s(s-a)(s-b)(s-c)}$
Calculate the terms $(s-a)$, $(s-b)$, and $(s-c)$:
$s - a = 21 - 18 = 3$ cm
$s - b = 21 - 10 = 11$ cm
$s - c = 21 - 14 = 7$ cm
Substitute these values into Heron's formula:
Area $= \sqrt{21 \times 3 \times 11 \times 7}$
Factorize the numbers inside the square root:
Area $= \sqrt{(3 \times 7) \times 3 \times 11 \times 7}$
Group the common factors:
Area $= \sqrt{3^2 \times 7^2 \times 11}$
Take the terms with squares out of the square root:
Area $= 3 \times 7 \times \sqrt{11}$
Area $= 21\sqrt{11}$ cm$^2$
The area of the triangle is $21\sqrt{11}$ cm$^2$.
Question 5. Sides of a triangle are in the ratio of 12 : 17 : 25 and its perimeter is 540 cm. Find its area.
Answer:
Given:
The ratio of the sides of the triangle is $12 : 17 : 25$.
The perimeter of the triangle is $540$ cm.
To Find:
The area of the triangle.
Solution:
Let the sides of the triangle be $12x$, $17x$, and $25x$ for some positive constant $x$.
The perimeter of the triangle is the sum of its sides.
Perimeter $= 12x + 17x + 25x$
We are given that the perimeter is $540$ cm.
$540 = 12x + 17x + 25x$
$540 = (12 + 17 + 25)x$
$540 = 54x$
To find the value of $x$, divide both sides by 54:
$x = \frac{540}{54}$
$x = 10$
Now, we can find the actual lengths of the sides:
Side 1 ($a$) $= 12x = 12 \times 10 = 120$ cm
Side 2 ($b$) $= 17x = 17 \times 10 = 170$ cm
Side 3 ($c$) $= 25x = 25 \times 10 = 250$ cm
Next, calculate the semi-perimeter ($s$), which is half of the perimeter.
$s = \frac{\text{Perimeter}}{2}$
$s = \frac{540}{2}$
$s = 270$ cm
We use Heron's formula to find the area of the triangle:
Area $= \sqrt{s(s-a)(s-b)(s-c)}$
Calculate the terms $(s-a)$, $(s-b)$, and $(s-c)$:
$s - a = 270 - 120 = 150$ cm
$s - b = 270 - 170 = 100$ cm
$s - c = 270 - 250 = 20$ cm
Substitute these values into Heron's formula:
Area $= \sqrt{270 \times 150 \times 100 \times 20}$
Area $= \sqrt{(27 \times 10) \times (15 \times 10) \times (100) \times (2 \times 10)}$
Area $= \sqrt{27 \times 15 \times 2 \times 10 \times 10 \times 100 \times 10}$
Area $= \sqrt{(3^3) \times (3 \times 5) \times 2 \times 10^4}$
Area $= \sqrt{3^4 \times 5 \times 2 \times 10^4}$
Area $= \sqrt{3^4 \times 10 \times 10^4}$
Area $= \sqrt{3^4 \times 10^5}$
Let's try factoring the original numbers for simplification:
Area $= \sqrt{270 \times 150 \times 100 \times 20}$
Area $= \sqrt{(27 \times 10) \times (15 \times 10) \times (10 \times 10) \times (2 \times 10)}$
Area $= \sqrt{(3 \times 3 \times 3 \times 2 \times 5) \times (3 \times 5 \times 2 \times 5) \times (2 \times 5 \times 2 \times 5) \times (2 \times 2 \times 5)}$
Count the prime factors:
Number of 2s: 1 + 1 + 2 + 2 = 6
Number of 3s: 3 + 1 = 4
Number of 5s: 1 + 2 + 2 + 1 = 6
Area $= \sqrt{2^6 \times 3^4 \times 5^6}$
Area $= 2^{6/2} \times 3^{4/2} \times 5^{6/2}$
Area $= 2^3 \times 3^2 \times 5^3$
Area $= 8 \times 9 \times 125$
Area $= 72 \times 125$
$72 \times 125 = 72 \times \frac{1000}{8} = 9 \times 1000 = 9000$
Area $= 9000$ cm$^2$
The area of the triangle is $9000$ cm$^2$.
Question 6. An isosceles triangle has perimeter 30 cm and each of the equal sides is 12 cm. Find the area of the triangle.
Answer:
Given:
The perimeter of an isosceles triangle is $30$ cm.
Each of the equal sides is $12$ cm.
To Find:
The area of the triangle.
Solution:
Let the equal sides of the isosceles triangle be $a = 12$ cm and $b = 12$ cm. Let the third side be $c$ cm.
The perimeter of the triangle is the sum of its sides.
Perimeter $= a + b + c$
We are given the perimeter is $30$ cm, and $a = 12$, $b = 12$.
$30 = 12 + 12 + c$
... (i)
$30 = 24 + c$
To find the length of the third side $c$:
$c = 30 - 24$
$c = 6$ cm
The lengths of the sides of the triangle are $12$ cm, $12$ cm, and $6$ cm.
Next, we calculate the semi-perimeter ($s$), which is half the perimeter.
$s = \frac{\text{Perimeter}}{2}$
$s = \frac{30}{2}$
$s = 15$ cm
To find the area of the triangle, we use Heron's formula:
Area $= \sqrt{s(s-a)(s-b)(s-c)}$
First, calculate $(s-a)$, $(s-b)$, and $(s-c)$:
$s - a = 15 - 12 = 3$ cm
$s - b = 15 - 12 = 3$ cm
$s - c = 15 - 6 = 9$ cm
Now, substitute these values into Heron's formula:
Area $= \sqrt{15 \times 3 \times 3 \times 9}$
Area $= \sqrt{(3 \times 5) \times 3^2 \times 3^2}$
Area $= \sqrt{3 \times 5 \times 9 \times 9}$
Area $= \sqrt{3 \times 5 \times 81}$
Area $= \sqrt{81 \times 15}$
Area $= \sqrt{81} \times \sqrt{15}$
Area $= 9\sqrt{15}$ cm$^2$
The area of the isosceles triangle is $9\sqrt{15}$ cm$^2$.

